This problem is popular on social media, and I thank everyone who sent it to me. I give extra thanks to Chaitanya from India who was the first person to send it to me.

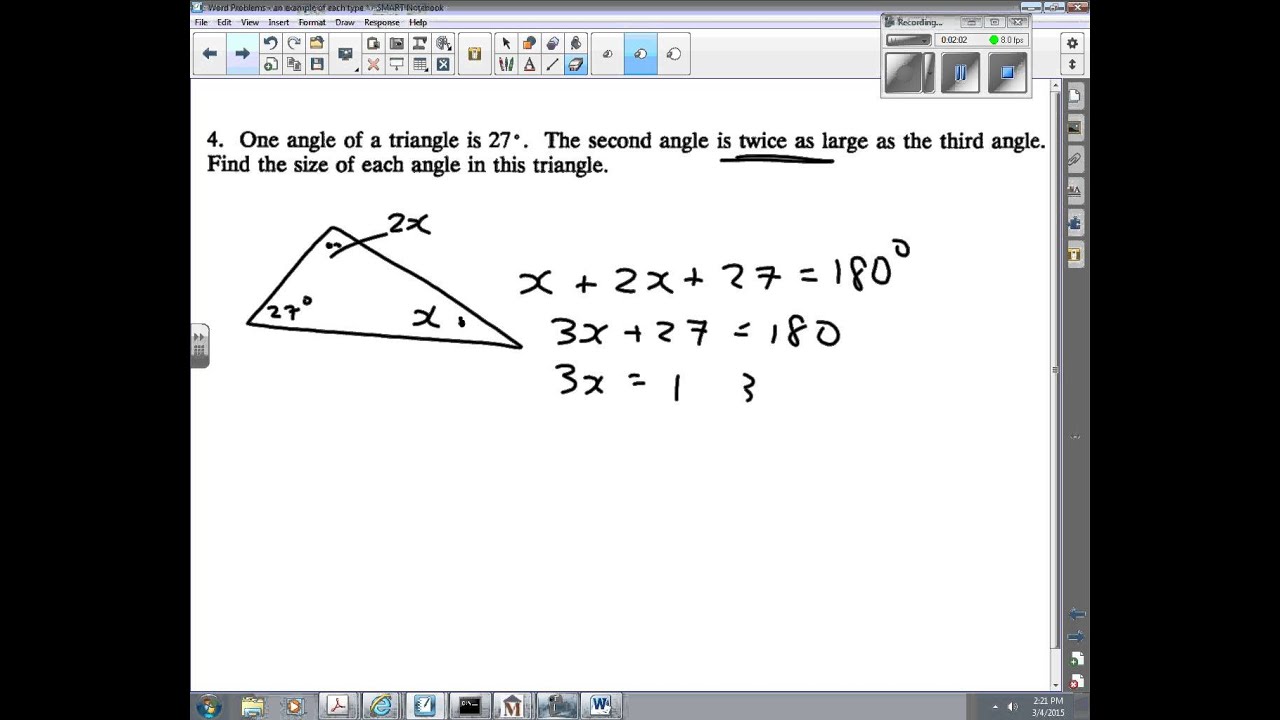
Solve the above quadratic equation for W and substitute to find L W = 3 and L + 6 Let r be the radius of the disk. Area is known and equal to 100π; hence 100π = π r 2 Solve for r: r = 10 Circumference = 2 π r = 20 π Let r be the radius of the semicircle. Area of the semicircle is known; hence. If you want to solve geometry problems, we have qualified and experienced experts who can help you. They will present the subject in a way that you will understand it. Feel free to get in touch with our math problem solver geometry in case you have any questions that need answers. Our customer support is available 24/7 when you need help. Guideline to follow while using the free math problem solver. As you enter your math problems, the solver will show you the Math Format automatically to make sure you have effectively entered the math problem you really want it to solve. You cannot enter word problems since the. Solving geometry problems gives students much needed geometry practice and strengthens their logical thinking, problem solving and analytical skills. It also helps teachers gauge how well students have understood the geometric concepts, and identify the areas in which extra help is needed.

In the following figure, ABCD is a square with a side of 10, APD and CPD are semicircles, and ADQB is a quarter circle. The problem is to find the shaded area DPQ.

Watch the video for a solution.

Or keep reading.
.
.

'All will be well if you use your mind for your decisions, and mind only your decisions.' Since 2007, I have devoted my life to sharing the joy of game theory and mathematics. MindYourDecisions now has over 1,000 free articles with no ads thanks to community support! Help out and get early access to posts with a pledge on Patreon.

.
.
.
.
.
.
M
I
N
D
.

Online Math Problem Solver - Math10.com

Y
O
U
R
.
D
E
C
I
S
I
O
N

Reference

S
.
P
U
Z
Z
L
E
.
.
.
.
Answer To Solve For The Shaded Area – Challenging Geometry Problem

(Pretty much all posts are transcribed quickly after I make the videos for them–please let me know if there are any typos/errors and I will correct them, thanks).

I found the problem to be fairly challenging. I ultimately solved it by using calculus and solving integrals, which can be seen here on Desmos. But I figured there must be a way using geometry and trigonometry, as it was so popular on social media. So I posted the problem to Math StackExchange, and within a few hours David K, Achille Hui, and Seyed posted replies that helped me understand. I thank them for the geometry and trigonometry solutions presented below.

I will present 3 ways to solve the problem. First I will do the short way using geometry/trigonometry, then I will present a longer way with geometry/trigonometry, and finally I will present the calculus method.

Method 1: Short way geometry/trigonometry

The trick is seeing the red area is equal to the area of one circle-circle intersection minus another circle-circle intersection (such circle-circle intersections make a shape of a “geometric lens.”)

To find the area of the blue and yellow shapes, let’s solve for the intersection of two semi-circles that are perpendicular to each other, one with radius a centered at (0, a) and another with radius b centered at (a, b). As shown below, the intersection area can be decomposed into the area of the circular segment of each circle. And each circular segment equals a circular sector minus a triangle.

The trick in this short method is we don’t calculate the area of each triangle. The area of both triangles together is equal to the area of the kite between the circle’s centers and the intersection points–this is the area of the kite divided by one of its diagonals. But we can also find the area of the kite from the two triangles of the other diagonals–and those areas are easier to calculate since those are right triangles with legs a and b (as the semi-circles intersect at right angles). So the area of the kite is ab/2 + ab/2 = a, and that needs to be subtracted from the area of the circular sectors.

The area of the circular sectors can be found by solving for the central angle in each circle. Let θ be the angle opposite side b in the right triangle, so then the angle opposite a is π/2 – θ.

In the diagram below, the angle θ is half of the central angle, and it equals arctan(b/a) in the right triangle. So the central angle for the sector with radius a is double θ, or 2 arctan(b/a), and the central angle for the radius with sector b is 2(π/2 – θ) = π – 2 arctan(b/a).

We then use the formula for the area of a circular sector to get the area of intersection:

b²(π – 2θ) + a²(2θ) – ab
(a² – b²) arctan(b/a) + πb²/2 – ab.

We can now use this general formula to derive the areas of the blue shape and yellow shape.

In the blue shape a = 10 and b = 5, so we have:

blue shape = (10² – 5²) arctan(5/10) + π(5)²/2 – (10)(5)
blue shape = 75 arctan(0.5) + 12.5π – 50

In the yellow shape a = b = 5

yellow shape = (5² – 5²) arctan(5/5) + π(5)²/2 – 5(5)
yellow shape = 12.5π(5)²/2 – 25

So we finally have:

red shape = (blue shape) – (yellow shape)
red shape = (75 arctan(0.5) + 12.5π – 50) – (12.5π(5)²/2 – 25)
red shape = 75 arctan(0.5) – 25 ≈ 9.77

Method 2: Long way geometry/trigonometry

In case you didn’t see the trick above, you might have instead solved for each circular segment individually. So let’s just do that method as it’s not too much longer, and it shows how to solve for the area of each triangle.

First we solve for the yellow area. Since the two circles have the same radius of 5, each half has an equal area. So we solve for one half and then double it:

The yellow shape has double the area calculated above, so it is:

yellow shape = 2(25π/4 – 25/2) = 12.5π – 12.5

We can then solve for the blue area by splitting its area into two circular segments.

The area of a circular segment is equal to the area of a circular sector minus the area of a triangle.

We now need to figure out the central angle, and we can do that with some trigonometry.

So from the above we see this circular segment is equal to:

0.5(10²)(2 arctan(0.5)) – 0.5(10²)(0.8)
100 arctan(0.5) – 40

We now calculate the area of the other circular segment in a similar fashion.

So from the above we see this circular segment is equal to:

0.5(5²)(π – 2 arctan(0.5)) – 0.5(5²)sin(π – 2θ)
12.5π – 25 arctan(0.5) – 12.5 sin(2θ)
12.5π – 25 arctan(0.5) – 10

So the total area of the blue shape is then:

blue shape = (100 arctan(0.5) – 40) + (12.5π – 25 arctan(0.5) – 10)
blue shape = 75 arctan(0.5) – 50 + 12.5π

We once again find the total area like in Method 1 as the area of blue shape minus that of the yellow shape.

red shape = (blue shape) – (yellow shape)
red shape = (75 arctan(0.5) + 12.5π – 50) – (12.5π(5)²/2 – 25)
red shape = 75 arctan(0.5) – 25 ≈ 9.77

Method 3: Calculus

I originally solved the problem using calculus, as the area bounded by three curves as seen in this image:

The middle integral can be solved as the area of a quarter circle with a radius of 5.

The other two integrals can be solved with trigonometric substitutions.

Those integrals all simplify to be:

50 arcsin(0.8) + 12.5 arcsin(0.6) – 25 – 6.25π ≈ 9.77

This is equivalent to the answer in the other methods, but I felt I should reconcile the two expressions. First we can notice 0.8 and 0.6 are complementary angles in a 3-4-5 right triangle, so:

arcsin 0.8 + arcsin 0.6 = π/2
hence
12.5 arcsin 0.8 + 12.5 arcsin 0.6 = 6.25 π

So our expression simplifies to:

50 arcsin(0.8) + 12.5 arcsin(0.6) – 25 – 6.25π
37.5 arcsin(0.8) + 12.5 arcsin(0.8) + 12.5 arcsin(0.6) – 25 – 6.25π
37.5 arcsin(0.8) + 6.25π – 25 – 6.25π
37.5 arcsin(0.8) – 25

Now we just need one more step, which uses the inverse trigonometric identity:

arcsin(x) = 2 arctan(x/(1 + √(1 – x²)

Thus we get

arcsin(0.8) = 2 arctan(0.5)

So finally we have:

37.5 arcsin(0.8) – 25
75 arctan(0.5) – 25 ≈ 9.77

And that is the same answer as the other methods!

Sources

Thanks to Chaitanya from India for sending me this problem.

Solve My Math Problem Geometry

Thanks to David K, Achille Hui, and Seyed on Math StackExchange for the geometry/trigonometry solutions.
https://math.stackexchange.com/questions/3016718/a-way-to-find-this-area-without-calculus

Desmos illustration of area between curves
https://www.desmos.com/calculator/jzuchfkmwl

How To Solve Math Problems Step-by-Step | Sciencing

Problem solving is not only the reason for teaching and learning mathematics. It is also the means for learning it. In the words of Hiebert et al:

Students should be allowed to make the subject problematic. … Allowing the subject to be problematic means allowing students to wonder why things are, to inquire, to search for solutions, and to resolve incongruities. It means that both curriculum and instruction should begin with problems, dilemmas, and questions for students. (Hiebert, et al, 1996, p. 12)

For years now, UP NISMED in-service training programs for teachers have organized mathematics lessons for teachers using the strategy we call Teaching through Problem Solving (TtPS). This teaching strategy had also been tried by teachers in their classes and the results far outweighed the disadvantages anticipated by the teachers.

Grade 9: Mathematics - Algebra II - Ron Paul Curriculum

Teaching through problem solving provides context for reviewing previously learned concepts and linking it to the new concepts to be learned. It provides context for students to experience working with the new concepts before they are formally defined and manipulated procedurally, thus making definitions and procedures meaningful to them.

What are the characteristics of a TtPS?

1. main learning activity is problem solving
2. concepts are learned in the context of solving a problem
3. students think about math ideas without having the ideas pre-explained
4. students solve problems without the teacher showing a solution to a similar problem first

What is the typical lesson sequence organized around TtPS?

1. An which can be solved in many ways is posed to the class.
2. Students initially work on the problem on their own then join a group to share their solutions and find other ways of solving the problem. (Role of teacher is to encourage pupils to try many possible solutions with minimum hints)
3. Students studies/evaluates solutions. (Teacher ask learners questions like “Which solutions do you like most? Why?”)
4. Teacher asks questions to help students make connections among concepts
5. Teacher/students extend the problem.

What are the theoretical underpinnings of TtPS strategy?

1. Vygotsky’s Zone of Proximal Development (ZPD)

Click here for sample lesson using Teaching through Problem Solving to teach the tangent ratio/function.

The best resource for improving one’s problem solving skills is still these books by George Polya.

Graphing Polar Equations. This Is Tutorial On Graphing Polar Equations By Hand, Or Sketching, To Help You Gain Deep Understanding Of These Equations. Several Examples With Detailed Solutions Are Pr...